Digital Fundamental IMP Question (Solved)

Digital Fundamental Question And Answers-(Lets Crack The Exam)

1. State and explain De Morgan’s theorems with truth tables. - Module No. 1| (4M)

1.De Morgan's First Theorem:-

Statement - The complement of a logical sum equals the logical product of the complements.

Logic equation - A+B¯=A¯.B¯A+B¯=A¯.B¯

Proof -

NOR gate is equivalent to bubbled AND gate.

2.De Morgan's Second Theorem:-

Statement - The complement of a logical product equals the logical sum of the complements.

Logic equation - A.B¯=A¯+B¯A.B¯=A¯+B¯

Proof -

NAND gate is equivalent to bubbled OR gate.

Truth Table to prove De Morgan's Theorem:-

2. Implement AND, OR, & EX-OR gates using NAND & NOR gates.- Module No. 1| (7M)

Implementation of EXOR Gate using Universal gates.

a) Using NAND Gates

b) Using NOR Gates

3. What is the race condition in JK flip-flop? - Module No. 3| (3M)

Race Around Condition in JK Flip-flop:

· For J-K flip-flop, if J=K=1, and if clk=1 for a long period of time, then output Q will toggle as long as CLK remains high which makes the output unstable or uncertain.

· This is called a race around condition in J-K flip-flop.

· We can overcome this problem by making the clock =1 for very less duration.

· The circuit used to overcome race around conditions is called the Master Slave JK flip flop.

Master Slave JK flip flop:

· Here two JK flip flops are connected in series.

· The first JK flip flop is called the “master” and the other is a “slave”.

· The output from the master is connected to the two inputs of the slave whose output is fed back to inputs of the master.

· The circuit also has an inverter other than the two flip flops.

· The Clock Pulse and inverter are connected because of which the flip flops get an inverted clock pulse.

· In other words, if CP=0 for a master flip-flop, then CP=1 for a slave flip-flop and vice versa.

4. Design 1 - bit Magnitude Comparator. - Module No. 3| (4M)

A Comparator is a combinational circuit that gives output in terms of A>B, A<B, and A=B. This is entirely expected from the name. A digital comparator’s purpose is to compare numbers and represent their relationship with each other.

A 1-bit comparator compares two single bits.

5. Explain following terms w.r.t Digital Logic Family.Module No. 1| (3M)

1.Propogation delay :

The output of a logic gate does not change its state instantaneously in response to the change in the state of its input.

There is a time delay between these two events ,which is called as the propogation delay . Thus propogation delay is defined as time delay between the instant application of an input pulse and the instant of occurrence of the corresponding output pulse

2.Fan-in:

Fan-in is defined as the number of input gate has. For example, a two input gate will have a fan-in equal to 2.

3.Fan Out :

Fan out is defined as the maximum number of the inputs of the same IC family that a gate can drive without falling outside the specified voltage limits.

Higher the fan out higher is the current supplying capacity of the gate.

4.Power dissipation :

Power dissipation is the amount of power drawn by the IC due to the current flowing current through the IC as a result of the applied voltage.

5.Figure of merit :

The figure of merit of a logic family is the product of power dissipation and propogation delay . It is called as speed power product . The speed is specified in seconds and power is specified in W . The figure of merit should be as low as possible .

The figure of merit is always a compromise between speed and power dissipation . This means if we reduce the propogation delay then the power dissipation will increase and vice - versa.

Figure of merit is always used as a common means for measuring and comparing the over all performance of different IC families.

6.Noise Margin :

Noise immunity is defined as the ability of logic circuit to tolerate the noise without causing any unwanted changes in the output.

A quantitative measure of noise immunity is called as noise margin.

6. Express the Boolean function F = A + B’C in a sum of minterms. - Module No. 1| (3M)

Let,A = A(B + B’) = AB + AB’

This function is still missing one variable, so

A = AB(C + C’) + AB'(C + C’) = ABC + ABC’+ AB’C + AB’C’

The second term B’C is missing one variable; hence,

Let,B’C = B’C(A + A’) = AB’C + A’B’C

Combining all terms, we have

F = A + B’C = ABC + ABC’ + AB’C + AB’C’ + AB’C + A’B’C

But AB’C appears twice, and

according to theorem 1 (x + x = x), it is possible to remove one of those occurrences. Rearranging the minterms in ascending order, we finally obtain

F = A’B’C + AB’C’ + AB’C + ABC’ + ABC

= m1 + m4 + m5 + m6 + m7

SOP is represented as Sigma(1, 4, 5, 6, 7)

UNSOLVED :

7. Reduce the expression F = A [ B + C’ (AB + AC’)’] - Module No. 1| (4M)

8. Simplify the following Boolean function by using the tabulation method. F (A, B, C, D) = Σ m (0, 1, 2, 8, 10, 11, 14, 15) - Module No. 1| (7M)

9. Using D & E as the MEV, Reduce F = A’B’C’ + A’B’CD + A’BCE’ + A’BC’E + AB’C + ABC + ABC’D’. - Module No. 1| (7M)

10. Simplify the Boolean function F (w, x, y, z) = Σ m (0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14)- Module No. 1| (3M)

11. Design a full adder and realize full adder using 3X8 Decoder and 2 OR gates.- Module No. 2| (7M)

The truth table of a full adder is shown in Table1

i. The A, B and Cin inputs are applied to 3:8 decoder as an input.

ii. The outputs of decoder m1, m2, m4 and m7 are applied to OR gate as shown in figure to obtain the sum output.

iii. Similarly outputs m3, m5, m6 and m7 are applied to another OR gate to obtain the carry output.

iv. Implement of full adder is shown in figure1.

12. Simplify the Boolean function F = A’B’C’ + B’CD’ + A’BCD’ + AB’C’ - Module No. 1| (3M)

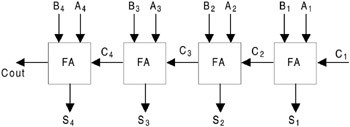
13. Explain 4 – bit parallel adder. - Module No. 3| (4M)

Consider the example that two 4-bit binary numbers B ₄B ₃B ₂B ₁ and A ₄A ₃A ₂A ₁ are to be added with a carry input C ₁. This can be done by cascading four full adder circuits as shown in Figure 5.48. The least significant bits A ₁, B ₁, and C ₁ are added to the produce sum output S ₁ and carry output C ₂. Carry output C ₂ is then added to the next significant bits A ₂ and B ₂ producing sum output S ₂ and carry output C ₃. C ₃ is then added to A ₃ and B ₃ and so on. Thus finally producing the four-bit sum output S ₄S ₃S ₂S ₁ and final carry output Cout. Such type of four-bit binary adder is commercially available in an IC package.